Для оценки частотных характеристик аналоговых электронных устройств (АЭУ) ввели понятие комплексный коэффициент усиления, который получают из передаточной функции АЭУ.
Комплексный коэффициент усиления по напряжению описывается зависимостью
$$\overset{\_}{\mathop{K}}\,=K(\omega )\,{{e}^{\text{j}\phi \text{(}\omega \text{)}}},$$
где \(K(\omega )=\sqrt{\operatorname{Re}_{{}}^{2}[K(j\omega )]+\operatorname{Im}_{{}}^{2}[K(j\omega )]}\) – модуль коэффициента усиления;
\(\phi (\omega )=arctg(\operatorname{Im}[K(j\omega )]/\operatorname{Re}[K(j\omega )])\) – аргумент коэффициента усиления, который является разностью фаз между входным и выходным сигналом.
Амплитудно-частотной (частотной) характеристикой (АЧХ) называется зависимость модуля коэффициента усиления \(K(\omega )~\)от частоты, при передаче гармонического сигнала, не вызывающего перегрузку.
Амплитудно-частотная характеристика усилительного каскада (рис. 1.5, в) изображена на рис. 1, а, где по горизонтали отложена частота \(f~=\omega /2\pi \), где \(\omega \) – угловая частота.
На практике чаще всего на АЧХ по вертикальной оси используют относительный масштаб, откладывая относительное усиление (рис. 1, а)
$$y(f)=\frac{K(f)}{{{K}_{0}}(f)}, \qquad\qquad\qquad\qquad (1)$$
т. е. коэффициент усиления, отнесенный к его значению на средних частотах, такая АЧХ называется нормированной.
Как правило, частоты, на которых относительное усиление уменьшается до условного уровня отсчета \(d=1/\sqrt{2}=0.707\), называются граничными частотами (в технической литературе встречается термин частоты среза) усилителя: \({{f}_{н}}\) и \(~{{f}_{в}}\) – соответственно нижняя и верхняя.
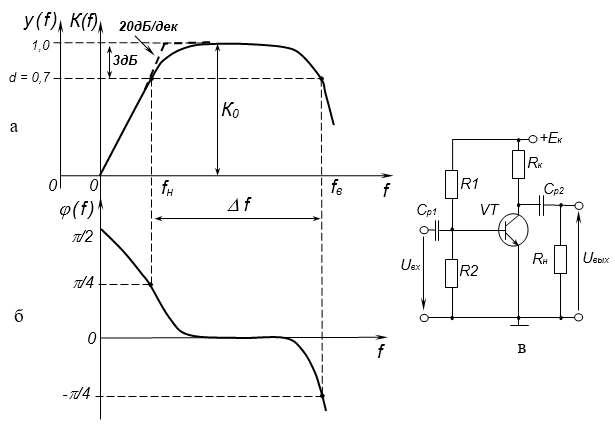
Рис. 1
Для АЧХ (рис. 1, а) типичным является наличие следующих участков:
область низких частот (область между \( 0<{f}<{{f}_{н}}\) );
область средних частот (область между \({{f}_{н}}\) и \(~{{f}_{в}}\)), в которой коэффициент усиления \(K(\omega )~\)почти не зависит от частоты и обозначается \({{K}_{0}}\);
область верхних частот (область между \({{f}_{в}}\ge f<\infty \));
Полосой пропускания усилителя \(\Delta f\) называют диапазон частот от \({{f}_{н}}\) до \(~{{f}_{в}}\).
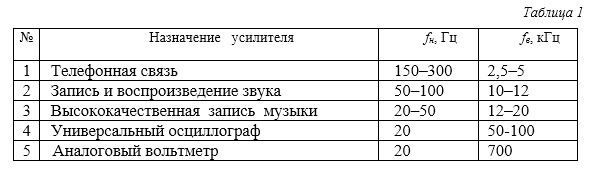
В табл. 1 приведены ориентировочные данные диапазона рабочих частот некоторых типов усилителей гармонических сигналов.
Вследствие спада усиления на краях полосы пропускания не все спектральные составляющие сложного колебания усиливаются в одинаковое число раз. Это приводит к искажениям его формы, которые называются амплитудно-частотными, или частотными искажениями.
Данные искажения принято оценивать, используя коэффициент частотных искажений \(\), который обычно определяют на граничной частоте (уровень \(d=0,707\)):
$$M=\frac{{{K}_{0}}}{{{K}_{f\,н,в}}}=\frac{1}{d}=\frac{1}{0,707}=1,41$$
и выражают в децибелах
\({{M}_{\left[дБ \right]}}=~20~lgM=~20~lg1,41\text{ }=\text{ }3~дБ\).
В ряде случаев допустимое значение \(M\) на граничных частотах имеет другое значение. Например, в усилителях измерительных приборов \(M\) принимают \(0,1~дБ\) и менее.
Частотные искажения воспринимаются на слух как изменение тембра (высоты тона).
Комплексный коэффициент усиления наряду с модулем также характеризуется и аргументом [фазой \(j(\omega )\)] .
Фазочастотной характеристикой (ФЧХ) называют зависимость фазового сдвига \(\varphi \) между входным и выходным сигналом от частоты, вносимого усилителем (рис. 1,б).
Для сложного сигнала (например, прямоугольного импульса) время прохождения его спектральных составляющих, через усилитель различно. Это приводит к искажениям формы сложного сигнала, которые называются фазочастотными, или фазовыми искажениями.
Фазочастотные искажения в усилителе получили название линейные искажения, так как создаются емкостями и индуктивностями схемы, которые являются линейными элементами.
Линейные искажения изменяют форму лишь сложного колебания, а на форму гармонического колебания не влияют.
Масштаб по оси частот на АЧХ и ФЧХ обычно берется логарифмический. Он удобен тем, что растягивает область нижних и сжимает область верхних частот. Это позволяет одинаково подробно рассматривать равные относительные изменения частоты в любой ее области.

