Технические показатели (показатели) любого электронного устройства представляют количественную оценку его свойств (усиление, искажения, точность преобразования, уровни сигналов на входе и выходе и т. д.) и позволяют оценить степень функциональной пригодности устройства.
В первую очередь рассмотрим технические показатели усилителей как основного типа АЭУ. Большинство их параметров могут быть отнесены и к другим аналоговым устройствам, выполняемым на основе усилителей.
Для описания основных показателей аналоговых электронных устройств используем функциональную схему усилителя на основе генератора напряжений (рис. 1).
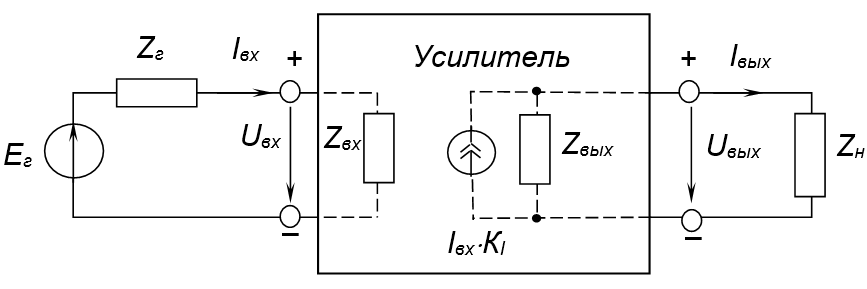
Рис. 1
Входное сопротивление усилителя \({{Z}_{вх}}\) – это внутреннее сопротивление между его входными зажимами.
В большинстве случаев входное сопротивление может быть представлено в виде параллельного соединения активного (резистивного) сопротивления \({{R}_{}}\) и емкости \({{C}_{}}\) (рис. 2).
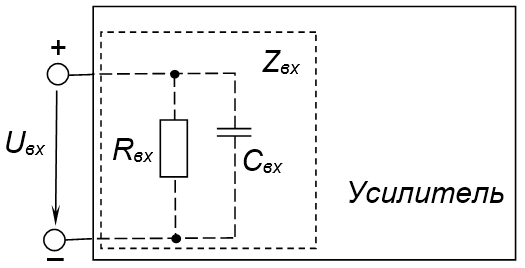
Рис. 2
Из рис. 2 следует, что общее входное сопротивление определятся согласно выражению \({{Z}_{вх}}={{R}_{вх}}//{{X}_{C}}\),
где $${{X}_{C}}=\frac{1}{j\omega {{C}_{вх}}}. \qquad\qquad\qquad\qquad(1.1)$$
Из выражения (1.1) следует, что чем меньше входная емкость, тем на большей частоте может работать усилитель. Поэтому при проектировании АЭУ обычно стремятся добиться большого входного сопротивления \({{R}_{вх}}\) при малой входной емкости \({{C}_{вх}}\). Это обеспечивает вопросы согласования АЭУ и их работу на высоких частотах.
Выходное сопротивление усилителя \({{Z}_{вых}}\) – это внутреннее сопротивление между его выходными зажимами, или
$${{{Z}}_{{вых}}}=\frac{\Delta {{U}_{вых}}}{\Delta {{I}_{{вых}}}}.$$
По отношению к нагрузке усилитель является источником сигналов, внутреннее сопротивление которого как раз равно \({{Z}_{вых}}\). В области средних частот выходное сопротивление можно считать активным. Если усилитель работает на нагрузку, подключаемую через коаксиальный кабель, с которым она согласована, \({{R}_{вых}}\) должно равняться характеристическому сопротивлению кабеля (обычно 75 Ом или 50 Ом) во избежание отражений, приводящих к потерям мощности и искажениям формы импульсов.
Для усилителей звуковой частоты желательно, чтобы их выходное сопротивление было как можно меньше. Это ослабляет зависимость выходного напряжения от сопротивления нагрузки. Последнее свойство особенно важно для усилителей, работающих на нестабильную нагрузку, например трансляционную сеть звукового вещания.
Для оценки данного свойства усилителя применяются специальные показатели:
коэффициент демпфирования \({{k}_{д}}={{R}_{н}}/{{R}_{вых}}\)
коэффициент сброса нагрузки \({{k}_{с}}{{=}_{{}}}|{{U}_{вых.хх}}/{{U}_{вых}}|=|1{ }+{ }({{Z}_{вых}}/{{Z}_{н}})|\).
Коэффициент усиления \({{K}_{u}}(K)\)(передачи напряжения усилителя) – это отношение амплитуды его выходного переменного гармонического напряжения к амплитуде входного (рис. 2)
$${{K}_{{u}}}=\frac{{{U}_{вых}}}{{{U}_{{вх}}}}. \qquad\qquad\qquad\qquad(1.2)$$
Коэффициент усиления по напряжению определяется в установившемся режиме при гармоническом (синусоидальном) входном сигнале. Данный коэффициент используется наиболее часто при оценке технических свойств АЭУ и в технической литературе часто обозначается через \(K\)(без индекса «u»).
Коэффициентом сквозной передачи \({{K}_{ск}}\left( {{K}^{*}} \right)\), или сквозным коэффициентом передачи по напряжению, называют отношение
$${{K}_{{ск}}}({{K}^{*}})=\frac{{{U}_{вых}}}{{{E}_{{г}}}}.$$
Анализ рис. 2 показывает, что сквозной коэффициент передачи можно записать
$${{K}_{ск}}=\frac{{{U}_{вых}}}{{{U}_{вх}}+{{U}_{Z}}_{г}}=\frac{{{U}_{вых}}}{{{U}_{вх}}+{{I}_{вх}}{{Z}_{г}}}. \qquad\qquad\qquad\qquad(1.3)$$
Однако для эквивалентного генератора входного напряжения допустимо считать \({{Z}_{}}\to 0\), следовательно, выражение (1.3) будет иметь вид
$${{K}_{ск}}=\frac{{{U}_{вых}}}{{{U}_{вх}}+{{I}_{вх}}{{Z}_{г}}}\approx \frac{{{U}_{вых}}}{{{U}_{вх}}}\approx {{K}_{u}}.$$
Для вывода коэффициента усиления по току рассмотрим структуру усилительного устройства, где входной сигнал представлен в виде эквивалентного генератора тока (рис. 3).
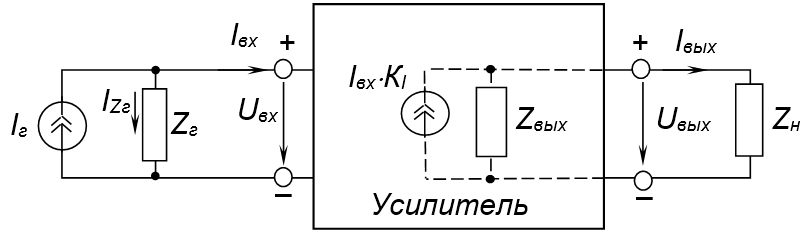
Рис. 3
Коэффициентом усиления по току \({{K}_{i}}_{{}}\)– это отношение амплитуды его выходного переменного гармонического тока к амплитуде входного
$${{K}_{i}}=\frac{{{I}_{вых}}}{{{I}_{вх}}}. \qquad\qquad\qquad\qquad(1.4)$$
На практике коэффициент усиления по току используется реже, так как для измерения токов требуется осуществлять разрыв цепей, что трудоемко.
Сквозным коэффициентом усиления тока \({{K}_{i}}_{ск}\) называется отношение
$${{K}_{i\,}}=\frac{{{I}_{вых}}}{{{I}_{вх}}}.$$
Так как для эквивалентного генератора тока выполняется условие \({{Z}_{г}}\to \infty \), а \({{I}_{Z}}_{г}\to 0~\) (рис. 1), то можно записать
$${{K}_{iск}}=\frac{{{I}_{вых}}}{{{I}_{вх}}+{{I}_{Zг}}}\approx \frac{{{I}_{вых}}}{{{I}_{г}}}={{K}_{i}}.$$
Коэффициентом усиления мощности \({{K}_{p}}\) называют отношение мощности усиленного сигнала в нагрузке к мощности, подаваемой на вход усилителя:
$${{K}_{}}=\frac{{{P}_{н}}}{{{P}_{вх}}}, \qquad\qquad\qquad\qquad(1.5)$$
где
$${{P}_{н}}={{I}_{вых}}\cdot {{U}_{вых}}=I_{вых}^{2}\cdot {{R}_{н}}=\frac{U_{вых}^{2}}{{{R}_{н}}},$$
а
$${{P}_{вх}}={{I}_{вх}}\cdot {{U}_{вх}}=I_{вх}^{2}\cdot {{R}_{вх}}=\frac{U_{вх}^{2}}{{{R}_{вх}}}.$$
При условии, что нагрузка и входное сопротивление носят активный характер.
В связи с тем что слуховое восприятие звукового сигнала пропорционально логарифму модуля коэффициента усиления по мощности, то для сравнения мощностей двух колебаний была введена логарифмическая единица – бел (названа по имени изобретателя телефона А. Белла).
Коэффициент усиления мощности часто выражают в более мелких единицах – децибелах: \({{K}_{p}}_{\left[ дб\right]}=~10~lg{{K}_{p}}\).
Логарифмические единицы удобны тем, что позволяют уменьшить количество знаков, а перемножение коэффициентов усиления заменить сложением.
Если мощности \({{P}_{н}}\) и \({{P}_{вх}}\) выделяются на одинаковых сопротивлениях (\({{R}_{н}}={{R}_{вх}}=R\)), то их отношение в децибелах можно выразить через отношение напряжений
$${{K}_{p[дб]}}=10\lg \frac{{{U}^{2}}_{вых}/{R}}{{{U}^{2}}_{вх}/R}=20\lg \frac{{{U}_{}}}{{{U}_{}}}=20\lg {{K}_{u}},$$
следовательно $${{K}_{[дб]}}=20\lg {{K}_{u}}, \qquad\qquad\qquad\qquad(1.6)$$
а или тока $${{K}_{p[дб]}}=10\lg \frac{{{I}^{2}}_{вых}R}{{{I}^{2}}_{вх}R}=20\lg \frac{{{I}_{вых}}}{{{I}_{вх}}}=20\lg {{K}_{i}},$$
тогда $${{K}_{i[дб]}}=20\lg {{K}_{i}}. \qquad\qquad\qquad\qquad(1.7)$$
Эту запись \({{K}_{u}}\) и \({{K}_{i}}\) в децибелах используют даже при \({{R}_{н}}\ne {{R}_{вх}}\), хотя это и не совсем корректно.
Например, если напряжение на нагрузке усилителя 40 В, а его входное напряжение 0,004 В, то коэффициент усиления в относительных единицах
$${{K}_{u}}=\frac{{{U}_{вых}}}{{{U}_{вх}}}=~40{ }/0,004~=~10000,$$
а в децибелах \({{K}_{\left[дБ\right]}}=~20~\lg {{K}_{u}}={ }20~lg10000~=~80\).
Например, определить коэффициент усиления двухкаскадного усилителя в децибелах, если усиление каскадов по напряжению \({{K}_{1[дБ]}}={ }5~\), а \({{K}_{2[дБ]}}={ }0,6~\).
Решение
Определим общий коэффициент усиления в децибелах согласно выражению
$${{K}_{[ дБ]}}={ }{{K}_{1[дБ]}}+{ }{{K}_{2[дБ]}}={ }5~+{ }{{0,6}_{~}}=~5,6.$$
Если, наоборот, известно, что коэффициент усиления в децибелах, то усиление в относительных единицах будет определяться по формулам:
$${{K}_{u}}={{10}^{0,05{{K}_{u[дБ]}}}};$$
$${{K}_{i}}={{10}^{0,05{{K}_{i[дБ]}}}};$$
$${{K}_{p}}={{10}^{0,1{{K}_{p[дБ]}}}}.$$
Перевод коэффициентов усиления по мощности и напряжению (току) из децибел в безразмерные единицы приведен в табл. 1.1.
Например, известно, что коэффициент усиления по напряжению в децибелах равен \({{K}_{u\left[дБ\right]}}=60~ дБ \), то его величина в относительных единицах будет равна \({{K}_{u}}~=~{{10}^{~(0,05\times 60)}}={{10}^{3}}=~1000\).
Например, определить коэффициент усиления двухкаскадного усилителя в децибелах и безразмерных единицах, если усиление каскадов по напряжению \({{K}_{u1\left[дБ\right]}}={ }3~\), а \({{K}_{u2\left[дБ\right]}}={ }0,7~\).
Решение
Определим общий коэффициент усиления в децибелах согласно выражению
\({{K}_{u\left[дБ\right]}}={ }{{K}_{u1\left[дБ\right]}}+{ }{{K}_{u2\left[дБ\right]}}={ }3~+{ }{{0,7}_{~}}=~3,7\).
Для определения общего коэффициента усиления в безразмерных единицах необходимо:
а) коэффициенты усиления каскадов из децибел перевести в безразмерные единицы, используя табл. 1, тогда \({{K}_{u1}}~={ }1,412538\), \({{K}_{u2}}={ }1,083927\);
б) определить общий коэффициент усиления, используя зависимость \(K~={ }{{K}_{u1}}\times {{K}_{u2}}~={ }1,531088\).
Таблица 1

Рис. 3
На практике в ряде случаев децибел используют для определения не величины отношения двух сигналов, а абсолютного значения амплитуды выходного сигнала. С этой целью используют ряд эталонных значений, что позволяет определять выходную амплитуду и усиление в децибелах по отношению к эталонной.
В радиоэлектронике для оценки параметров усилителя (приемника) эталонным входным напряжением принято считать \(1{мВ}\), а если оценка проводится по мощности – \(1{мВт }\).
При оценке чувствительности приемника, в основном, используются следующие эталоны:
при длине волны \(\lambda \le 50{ }\) за эталон входного сигнала принимают \(1{мВт}\);
при длине волны \(\lambda \ge 50{ }\) за эталон входного сигнала принимают \(1{ мВ}\).
Пример 1.1. Определить минимальную амплитуду входного сигнала \({{P}_{пр.}}_{min}\) на входе приемника (\(\lambda \le 50{см}\), т. е. \({{P}_{э}}={ }1{мВт}\)), если чувствительность приемника равна \({{P}_{пр\left[дБ \right]}}=~-80{дБ}\).
Решение
а) определяем чувствительность в относительных единицах, используя табл. 1.1 или выражение
$${{P}_{пр}}={{10}^{0,1{{P}_{пр[дБ]}}}}={{10}^{0,1\times (-80)}}={{10}^{-8}}.$$
б) определяем минимальную амплитуду входного сигнала на входе приемника, если эталонное значение равно \({{P}_{э}}={ }1{мВт}\)
$${{P}_{пр}}=\frac{{{P}_{пр.{min}}}}{{{P}_{{э}}}}={{10}^{8}}.$$
Из данного выражения следует, что минимальная амплитуда входного сигнала будет равна
$${{P}_{{пр.min}}}={{P}_{пр}}\cdot {{P}_{э}}={{10}^{-11} Вт }\ .$$
Наряду с децибелами ранее использовали и другую логарифмическую единицу – непер (Нп). Усиление, выраженное в неперах, представляет собой натуральный логарифм численного значения \(K\), выраженного в безразмерных единицах \({{K}_{[Нп]}}=~\ln K\). Между данными единицами измерения коэффициентов усиления существуют следующие соотношения: \(1~{ дБ }={ }0,115~Нп\); \(1~{Нп }={ }8,7~ дБ \).
На практике данной единицей измерения не пользуются.
Коэффициент полезного действия (КПД) \(\eta \) характеризует экономичность расходования энергии питания усилителем.
Обычно КПД измеряется при усилении гармонического сигнала частоты 1 кГц.
Общий КПД усилителя представляет отношение номинальной выходной мощности, отдаваемой в нагрузку, к суммарной мощности, потребляемой им от всех источников питания \({{\eta }_{s}}={{P}_{н}}/{{P}_{s}}\).
Мощностью потерь \({{P}_{п}}\) называют разность между суммарной мощностью и мощностью, выделяемой на нагрузке: \({{P}_{п}}_{~}={{P}_{s}}-{{P}_{н}}\).
На практике часто применяется также КПД выходной цепи усилительного элемента, который представляет отношение мощности переменного тока, создаваемой в выходной цепи усилительного элемента (например транзистора), к полной потребляемой мощности от источника питания
$$\eta =\frac{{{P}_{\sim}}}{{{P}_{=}}+{{}_{\sim}}}=\frac{0,5{{U}_{вых\,}}\cdot {{I}_{вых\,}}}{({{U}^{0}}\cdot {{I}^{0}})+0,5({{U}_{вых\,}}\cdot {{I}_{вых\,}})}, \qquad\qquad\qquad\qquad(1.8)$$
где \({{U}^{0}}\) и \({{I}^{0}}\) – постоянные напряжение и ток покоя,
\({{U}_{вых}}\) и \({{I}_{вых}}\) – амплитуды выходного напряжения и тока.
Данный КПД учитывает потери мощности только на усилительном элементе и применяется для оценки экономичности оконечных каскадов как основных потребителей энергии питания.
Пример 1.2. Определить КПД выходного каскада, работающего в режиме А, если \({{U}^{0}}~={ }5{ }В\), \({{I}^{0}}^{{}}={ }4{ }мА\), а \({{U}_{вых}}={ }4{ }В\), \({{I}_{вых}}={ }2{ }мА\), \({{U}_{}}={ }4{ В}\)
Решение
КПД выходного каскада определим согласно выражению (1.8)
$$\eta =\frac{{{P}_{\sim}}}{{{P}_{=}}+{{}_{\sim}}}=\frac{0,5{{U}_{вых\,}}\cdot {{I}_{вых\,}}}{({{U}^{0}}\cdot {{I}^{0}})+0,5({{U}_{вых\,}}\cdot {{I}_{вых\,}})}=0,28,$$
а если КПД выразить в %, то \(\eta ={ }28\%\).
Чем выше КПД усилителя, тем меньше мощность потерь в нем, которая превращается в тепло, при заданной входной мощности.
Например, для предотвращения перегрева оконечных транзисторов их приходится снабжать радиаторами, размеры которых могут быть тем меньше, чем выше КПД.
Таким образом, КПД усилителя косвенно характеризует также его удельные размеры и массу (на единицу выходной мощности).
Экономичность питания усилителя оценивают по КПД и по току питания в режиме покоя (при отсутствии сигнала).

